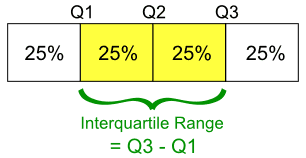
The "Interquartile Range" is from Q1 to Q3:
Example 1
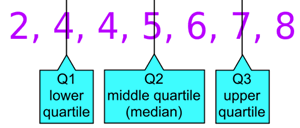
The Interquartile Range is:
Q3 - Q1 = 8 - 4 = 4
EXAMPLE 2
EXAMPLE 3:
Data set in a table
For the data in this table the interquartile range is IQR = 115 − 105 = 10.
Example 4:
The wheat production (in Kg) of 20 acres is given as: 1120, 1240, 1320, 1040, 1080, 1200, 1440, 1360, 1680, 1730, 1785, 1342, 1960, 1880, 1755, 1720, 1600, 1470, 1750, and 1885. Find the quartile devi ation.
Solution:
After arranging the observations in ascending order, we get
1040, 1080, 1120, 1200, 1240, 1320, 1342, 1360, 1440, 1470, 1600, 1680, 1720, 1730, 1750, 1755, 1785, 1880, 1885, 1960.
Q1=Value of (n+14)th item
=Value of (20+14)th item
=Value of (5.25)th item
=5th item+0.25(6th item−5th item)=1240+0.25(1320−1240)
Q1=1240+20=1260
Q3=Value of 3(n + 1)4th item
=Value of 3(20 + 1)4th item
=Value of (15.75)th item
=15th item+0.75(16th item−15th item)=1750+0.75(1755−1750)
Q3=1750+3.75=1753.75
1040, 1080, 1120, 1200, 1240, 1320, 1342, 1360, 1440, 1470, 1600, 1680, 1720, 1730, 1750, 1755, 1785, 1880, 1885, 1960.
Example 5:
Calculate the quartile deviation from the data given below:
Maximum Load
(short-tons) |
Number of Cables
|
Solution:
The necessary calculations are given below:
Maximum Load
(short-tons) |
Number of Cables
( |
Class
Boundaries |
Cumulative
Frequencies |
Where
Where



No comments:
Post a Comment